Lab 6: Geometric Correction

Goal and Background

The purpose of this lab was to practice geometric correction.  This was our first time working with the image preprocessing method.  This process is typical done before any information can be extracted from an image.  Geometric correction is performed because many satellite images are not collected in their proper planimetric position, also known as coordinates.  It does away with most of the distortion in the original satellite image and creates a more accurate images that we can use to extract reliable and accurate information.

In this lab we used:

• USGS 7.5 minute digital raster graphic image of the Chicago Metropolitan Statistical Area to correct a Landsat TM image of the same area.
• Landsat TM image for eastern Sierra Leone to correct a geometrically distorted image of the same area.

Methods

Part 1: Image-to-map rectification

In the first part of this lab we worked with the Chicago area.  We had a raster image that we needed to geometrically correct and a reference image which was a topographic map.  Two views were opened in order to view both images at once.  The distortion was visible, but not greatly so.  In order to create ground control points (GCPs) we needed to click on the Multispectral tab in order to activate the raster processing tools for multispectral imagery.  From here we chose the Control Points option.  We needed to click through some windows that opened in order to set parameters for the image.  Most of these we kept as their default settings.  One window that pops up tells us what coordinate system the images is in and it also says "model has no solution".  This means we need to add GCPs in order to create a solution for the model.

After clicking through multiple windows, we are now in the Multipoint Geometric Correction window.  On the left is the Chicago satellite image that needs to be corrected.  On the right is the Chicago reference image that is in the proper planimetric position.  Now we needed to create a minimum of three GCPs for this image because it has a 1st order of transformation.  There are different orders of transformation and in order to decide on which fits for an image we need to determine how many GCPs are needed in order to have a total RMS error below 1.  In the case of the Chicago images we need a minimum of three GCPs which means it is the first order of transformation.  Below in Figure 1 is a graph that was used in order to help determine that answer.  Also below in Figure 2 is how the two Chicago images were seen in the Multipoint Geometric Correction window.

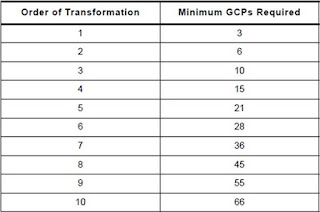Figure 1: Order of transformation table to help determine the minimum GCPs required.

Figure 2: Left satellite image of Chicago to be geometrically corrected. Right image of Chicago for a reference.

We created four GCPs which created the dialogue stating "Model solution is current".  In the results section is Figure 3 which shows the four GCPs and the total RMS error which is below 2.0.  Now that the image is geometrically corrected we needed to save the new image.  Also in the results section is Figure 4 which are side by side images of the original Chicago image and the corrected image.

Part 2: Image to image registration

For our next task we needed to geometrically correct and image with a reference image rather than a reference map like we used in part 1.  We imported the images in the same manner as in part 1, except for one part.  The Polynomial Model Properties window lets us choose the polynomial order for the image which sets the minimum amount of GCPs required to get the dialogue "Model solution is current".  Instead of a 1st order like we did in the part 1, we set it to the 3rd order.  This means we need a minimum of 10 GCPs in order to correct the image.

We created a total of 12 GCPs for these images and then made sure the RMS error was below 1, with below 0.5 being ideal.  In Figure 5 in the results section is an image of the twelve GCPs along with the total RMS error of 0.26.  One other thing we did differently with part 2 was when we saved the newly corrected image.  Instead of choosing nearest neighbor for the resampling process, we chose billinear interpolation.  We used this because it produces a more accurate image rather than using nearest neighbor.  The result of this correction is seen in Figure 6 in the results section.

Results

The Figures talked about earlier in this post are picture below here.

Figure 3: Four GCPs for the Chicago area with a total RMS error of 0.026

Figure 4: The original Chicago image is on the left.  The geometrically corrected image is on the right.

Figure 5: 12 GCPs for the Sierra Leone image with a total RMS error of 0.26.

Figure 6: The original image of Sierra Leone is on the left.  On the right is the geometrically corrected image.

I found that getting the total RMS error below 0.5 not to be very hard once I got the hang of how this process works.  In Figure 4, it is quite hard to tell the difference between the two images because they were not that different in the first place.  But, in Figure 6 there is quite a big difference.  The end image (on the right) turned out a bit distorted on the upper left portion.  I believe this is because most of my GCPs were focused in other areas.  If I could do it again I would put more GCPs in that area to get a more accurate and better looking result.  Also, it is quite obvious that some of the clarity was lost in the final image.  I don't know exactly as to why that is, but I am assuming it has to do with the type of interpolation that chose for that image.


Conclusions

Overall, this lab taught us a very valuable skill.  Given that many satellite images a not in their proper planimetric position, geometric correction needs to be done quite often.  Once it is practiced a couple of time the process becomes more understandable and practical.  It is vital to use this tool in order to get accurate data in the final product.

Lab 5: LiDAR Remote Sensing

Goal and Background

The main goal of this lab is to get basic knowledge of LiDAR data structure and processing.  This includes the processing of numerous surface and terrain images and then processing and creation of intensity image and other products from point cloud.

This is our first time working with LiDAR data and getting to know our way around using it.  LiDAR stand for light detection and ranging.  This method takes light in the form of a pulsing laser the measure ranges to Earth.  This data combined with other various data can help to generate 3D information about the shape of the Earth the characteristics of our planet.

Methods

Unlike our other labs, most of this lab was done in ArcMap instead of Erdas Imagine.  For the first part of the lab we needed to do a quality check of the LAS dataset we are given.  This entails checking the metadata and making sure everything looks correct.  After doing so, I had to create a new LAS dataset, this keeps the data organized and easily accessible when working with it.  Because we created a new dataset this means we need to build the statistics of the data.  The data already has statistics associated with it, but the new area does not have this data unless we calculate it.  Though, ArcCatalog does make this quite easier.  With the push of the 'calculate' button, all of the statistics are now in the LAS file.  The calculate button is sometimes too good to be true so we need to check the statistics to make sure they are correct.  The best way to do so is to check the elevation.  If the elevation is in the same range as the area the LiDAR data is taken of, then it's good to move onto the next step.  Our statistics are good so it's onto the next step.  Now we need to set the coordinate system for the data.  No coordinate system was imported with the LAS files so we need to look at the original to see if one of those files has the coordinate system the data was taken in.  It in fact does and now we need to transfer this to the new data.  Everything is set in ArcCatalog and it's time to move into ArcMap to actually work with the data.  

Once in ArcMap I imported the LAS dataset which is displayed in tiles until you zoom in to a certain extent and the LiDAR points are revealed.  I also added a shapefile of Eau Claire county to get a better grasp of where everything is.  Next I had to activate the LAS Dataset Toolbar in order to visualize the point clouds and generate different products for the next section of the lab.  I explored the different options I could change the map to look like.  For example, elevation, aspect, slope, and contour.  I also changed the filters that were available.  Here I couuld change which returns I wanted to see and which classes I wanted to see (ground, vegetation, building, water, etc).  After playing around with those options for a while, I moved onto creating two different rasters.  I created multiple DSMs and DTMs.  Figures 1 and 2 were created using hillshade.  Figure 1 shows the Eau Claire area with buildings and vegetation.  Figure 2 takes away all of that and just shows what the ground looks like without it all.  It was incredibly interesting to see what differences buildings and vegetation can make it a simple LiDAR image.  Figure 3 shows a LiDAR intensity image.  The intensity image shows the first return points from LiDAR.

Results

Below are the images I created using different tools throughout this lab.

Figure 1: Hillshaded image of the Eau Claire area.

Figure 2: Hillshaded image of Eau Claire without buildings or vegetation 

Figure 3: LiDAR intensity image

Conclusions

It was very interesting to see another side of remote sensing by learning about LiDAR.  I didn't know how diverse this area of study could really be.  I would like to learn more about LiDAR and all of it's capabilities.  I would also like to see if there are any health risks involved with the LiDAR lasers that are being sent down.  It will be interesting to see where LiDAR goes in the future and how it develops.

Lab 4: Miscellaneous Image Functions

Goal and Background

The main purpose of this lab is to:

• Define a study area from a larger satellite image
• Learn how spatial resolution of images can be enhanced for visual interpretation purposes
• Work with new radiometric enhancement techniques
• Linking satellite images with Google Earth 
• Learn methods of resampling satellite images
• Practicing methods of image mosaicking
• Learn binary change detection with the use of simple graphical modeling

Working with and learning these new skills are vital to the study of remote sensing.  These skills are practiced by using the ERDAS Imagine software.

Methods

Part 1: Image subsetting

• The first part of this lab worked with image subsetting and creating an area of interest (AOI) for a study area.  The AOI was created through using an inquire box.  The box was placed around the Eau Claire area and the subset was created.  This subset is pictured in Figure 1 below.

Figure 1: Eau Claire subset

• Next we created another subset, but we used a shape file in order to focus on a more specific AOI.  This was done by adding the shape file to the original raster that was used for the first subset.  The focused subset that was created is pictured below in Figure 2.

Figure 2: Eau Claire subset created with a shape file

Part 2: Image fusion

• In this section of the lab I created a higher spatial resolution image from a coarse resolution image.  This is done in order to enhance the image spatial resolution for visual interpretation functions.  First, I used the resolution merge tool in order to enhance the resolution from 30 meters in a reflective image to 15 meters from a panchromatic image.  This process resulted in a pan sharpened image with a resolution of 15 meters.  These three images are pictured in Figures 3.1, 3.2, and 3.3 below.

3.1: Panchromatic image, 15 meter resolution.

3.2: Reflective image, 30 meter resolution.

3.3: Pansharpened image, 15 meter resolution.

Part 3: Simple radiometric enhancement techniques

• This section focused on haze reduction in images.  I used the haze reduction tool and it enhanced the color of the image and overall clarity of it.  This tool is useful, but the resolution is not enhanced with the haze reduction. The original and haze reduced image are picture below in Figures 4.1 and 4.2.

Figure 4.1: Original image with haze.

Figure 4.2: Haze reduced image.

      

                                                                                              

Part 4: Linking image viewer to Google Earth

• I thought this part of the lab was very interesting.  It really showed the difference a high resolution satellite can make.  I opened an image of the Eau Claire area in ERDAS Imagine and opened another window that connected to Google Earth.  I synchronized the views and zoomed into where my house is in Eau Claire.  The image in ERDAS was completely pixelated and I couldn't make out any objects or significant features.  In the Google Earth window I could see my house clearly with no pixelation.  Google Earth uses GeoEye high resolution satellites and it's incredible the difference those satellites can make.  Zoomed out to their full extent these images look the same, but once you zoom in the differences are immediate.

Part 5: Resampling

• In this section I resampled an image with two different methods, nearest neighbor and bilinear interpolation.  The nearest neighbor and bilinear interpolation methods did not create a very noticeable difference compared to the original image.  The two processes had the pixel size changed from 30x30 to 15x15, which I thought would have made a big difference, but in the end the difference was not very noticeable unless you know what you're looking for.  I also debated about putting the three images in this blog post, but the differences are so indistinguishable at a large size that I decided not to include them.

Part 6: Image Mosaicking

• Two different types of mosaicking were used in this section, Mosaic Express and Mosaic Pro.  Mosaicking is basically taking two or more images and stitching them together in order to create on big image.  Mosaic Express is a quick and easy way to create one full image, but the final product does not look professional.  In order to get a better image I used Mosaic Pro.  This takes more effort and decisions to create, but ultimately the picture looks better overall and gives the user a better look at the two images as one.  The two mosaics are pictured below in Figures 5.1 and 5.2.

Figure 5.1: Mosaic created with Mosaic Express

Figure 5.2: Mosaic created with Mosaic Pro

Part 7: Binary change detection (image differencing)

• In the last section of the lab we used the model building tool.  The tool was quite simple and helped create the map pictured in Figure 6 below.  I inputted a map from August of 1991 and entered an equation to create an output to show pixel differentiation from August of 1991 to August of 2011.

Figure 6: Pixel changes from 1991 to 2011

Results

Pictured below are the images I created throughout this lab using different tools.

Figure 1: Eau Claire subset

Figure 2: Eau Claire subset created with a shape file

3.3: Pansharpened image, 15 meter resolution.

Figure 4.2: Haze reduced image.

Figure 5.1: Mosaic created with Mosaic Express

Figure 5.2: Mosaic created with Mosaic Pro

Figure 6: Pixel changes from 1991 to 2011

Conclusions

This lab really helped me learn more of the basic techniques used in ERDAS Imagine and in the study of remote sensing.  Knowing these simple tools allows me to critically look at remotely sensed images while also altering them in order to get the information I need.